Mathematik Die beste Wahl
Der Bundestag wird in 299 Wahlkreisen gewählt. Diese werden immer wieder mal verändert – wie, das steht im Wahlgesetz. Diese komplexe Aufgabe wird bisher per Hand gelöst. Mit einem mathematischen Modell ginge es viel besser
Stellen Sie sich vor, Sie sind Politikerin oder Politiker im Deutschen Bundestag. Bei der letzten Wahl hatten die Wählerinnen und Wähler in Ihrem Wahlkreis mehrheitlich das Kreuzchen neben Ihren Namen gesetzt. Nun sind Sie eine oder einer von 299 direkt gewählten Abgeordnetinnen und Abgeordneten im Parlament in Berlin. Sie mögen den Job – und schielen auf Ihre Wiederwahl. Doch die Stimmungslage in Ihrem Wahlgebiet macht Ihnen Sorgen. Die Menschen in den Städten halten weiterhin zu Ihnen, doch in den ländlichen Regionen macht sich zunehmend Enttäuschung breit. Ihr Wiedereinzug in den Bundestag ist gefährdet.
Da kommt Ihnen ein Gedanke: Was wäre, wenn Sie Ihren Wahlkreis so verändern, dass er weniger ländlich geprägt ist? Wie wäre es, die Grenzen des Wahlkreises zu verschieben und die Chancen auf eine Wiederwahl so zu steigern?
Tatsächlich werden vor jeder Wahl einzelne Änderungen an den 299 Wahlkreisen vorgenommen – und zwar vom Gesetzgeber, dem Deutschen Bundestag also. Die Regeln dafür legt das Wahlgesetz fest. Darin finden sich einerseits Vorgaben, die jeder Wahlkreis unbedingt einzuhalten hat. Zusätzlich gibt es Kriterien, die eine Wahlkreiseinteilung so gut wie möglich zu erfüllen hat, zum Beispiel, dass jeder Wahlkreis möglichst gleich viele Einwohnerinnen und Einwohner haben soll. Mathematisch gesehen entspricht diese Festlegung von Wahlkreisen einem sogenannten Optimierungsproblem. Wir wollten herausfinden, ob die aktuelle Einteilung im Sinne der Vorgaben bestmöglich ist, also ob Optimalität vorliegt.
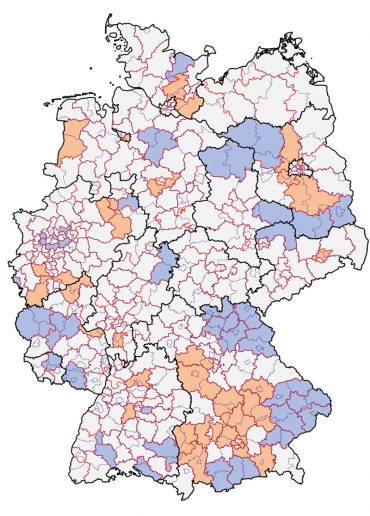
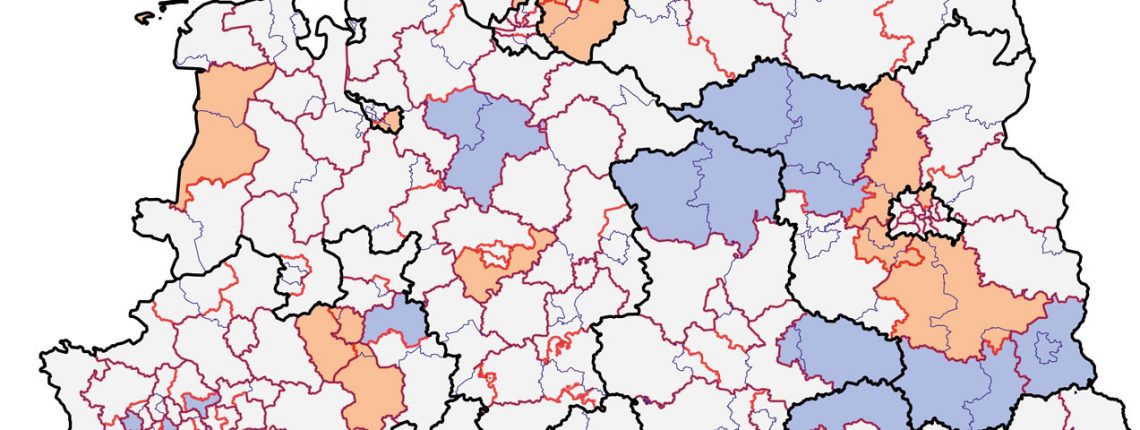
orange: bis 25 % über dem gesetzlichen Maximum
grau: gesetzliches Soll: weniger als 15 % Abweichung
blau: bis 25 % unter dem gesetzlichen Minimum
Ein Optimierungsproblem umfasst die Aufgabe, unter allen zulässigen Lösungen eine beste zu finden. Zulässig ist eine Lösung, wenn sie alle strikt zu erfüllenden Bedingungen einhält. So muss laut Gesetz ein Wahlkreis aus einem zusammenhängenden Gebiet bestehen und soll sich an bestehenden Verwaltungseinheiten wie zum Beispiel Landkreisen, Großstädten und Gemeinden orientieren. Die Menschen eines Wahlkreises sollen also nicht nur eine numerische Größe sein, sondern auch geografisch „ein zusammengehöriges und abgerundetes Ganzes“ bilden, wie das Bundesverfassungsgericht unterstrich. Außerdem sollen in jedem Wahlkreis mindestens 185.000 und höchstens 305.000 Deutsche leben.
Alle Lösungen, die diese Bedingungen erfüllen, sind zulässig. Welche nun die beste ist, bestimmen die Optimierungskriterien. Diese bewerten jede zulässige Lösung, dies erstellt eine Rangliste. An der Spitze des Rankings findet man eine Optimallösung. Eine solche zu ermitteln, ist das Ziel der Optimierung.
Unter diesen Voraussetzungen wollten wir nun eine optimale Einteilung der Wahlkreise für die Bundestagswahl berechnen – natürlich optimal nach Recht und Gesetz und nicht zur Verbesserung einer Wahlchance. Im ersten Schritt galt es, die im Wahlgesetz genannten Vorgaben in die Sprache der Mathematik zu überführen. Rein mathematisch kann dieses Gebietsplanungsproblem als eine Zerlegungsaufgabe einer abstrakten Struktur aus der „Graphentheorie“ interpretiert werden: Ein Graph repräsentiert eine Menge von Objekten und bestehende Verbindungen zwischen diesen. Die Objekte werden als Knoten bezeichnet, Verbindungen zwischen je zwei Knoten werden Kanten genannt. Unseren Graphen entwickeln wir ausgehend von einer Landkarte Deutschlands. Dies kann man grafisch veranschaulichen. Alle Städte werden in ihren Zentren mit einem Punkt markiert, das sind unsere Knoten des Graphen. Außerdem verbinden wir zwei Knoten mit einer Kante in Form einer geraden Linie, falls die zwei zugehörigen Gebiete benachbart sind. Nun lautet die abstrahierte Aufgabenstellung: Entferne Kanten des Graphen und zerlege so den Graphen in 299 Teilgraphen. Jeder Teilgraph wird anhand der Landkarte als einer der 299 Wahlkreise interpretiert.

Eine große, in der Forschung bisher unberücksichtigte Herausforderung hierbei war die Orientierung der Wahlkreise an bestehenden administrativen Grenzen. Um diese zu meistern, war Knobelarbeit angesagt. Wir skizzierten immer wieder neue Ideen und konstruierten Variablen und Gleichungen, mit deren Hilfe wir am Ende die Kriterien aus dem Gesetz in ein mathematisches Modell aus Entscheidungsvariablen, Nebenbedingungen und einer Zielfunktion überführen konnten.
Im nächsten Schritt galt es, ein Verfahren zu entwickeln, das eine optimale Wahlkreiseinteilung identifiziert, also unser aufgestelltes Optimierungsproblem löst. Auf den ersten Blick könnte man alle möglichen Graphzerlegungen der Reihe nach durchgehen, auf Zulässigkeit prüfen und auf diese Weise Stück für Stück eine Rangliste erstellen. Doch das ist selbst mit den leistungsstärksten Computern unmöglich, weil es für die Zerlegung des Graphen in Teilgraphen unvorstellbar viele Kombinationen gibt – nämlich mehr, als es Atome im Universum gibt. Und das sind immerhin etwa 1085 Stück.
Bei einer derartigen kombinatorischen Explosion kann die „Theorie der gemischt-ganzzahligen linearen Optimierung“ helfen. Bei dieser algorithmischen Suche nach einer Optimallösung wird der Lösungsraum abschnittsweise durchforstet. Dieser Raum umfasst alle durch das mathematische Modell beschriebenen Lösungen. Das Geheimnis: Es können Schritt für Schritt Teile des Lösungsraumes ausgeschlossen werden, ohne die enthaltenen Lösungen im Einzelnen anschauen zu müssen. Vor Betreten eines neuen Teilraumes kann abgeschätzt werden, wie gut eine beste Lösung in diesem Abschnitt sein kann. Hat der Algorithmus zuvor, in einem anderen Abschnitt, schon eine bessere Lösung gefunden, kann dieser Teilraum ignoriert werden. Schlussendlich müssen auf diese Weise nur vergleichsweise wenige zulässige Lösungen genauer betrachtet werden.
Die Erkenntnis unserer Arbeit: Die rechtlichen Kriterien lassen sich mithilfe unseres Modells besser erfüllen, als es bis jetzt der Fall war. In der Praxis werden Wahlkreise für die Bundestagswahl bisher per Hand eingeteilt, wobei ausgeglichenen Bevölkerungszahlen zwischen den Wahlkreisen eine eher untergeordnete Rolle beigemessen wird. Die teilweise hohen Abweichungen wurden sogar schon von internationalen Wahlbeobachterinnen und -beobachtern der Organisation für Sicherheit und Zusammenarbeit in Europa (OSZE) kritisiert. Den Entscheidungsträgerinnen und -trägern im Deutschen Bundestag ist indes wichtiger, dass sich Wahlkreise an Verwaltungsgrenzen von Landkreisen, Großstädten und Ähnliches orientieren. Dieses Ziel erfüllen die gegenwärtigen Wahl-kreise sehr gut. Unsere Forschung zeigt aber, dass sich darüber hinaus auch das Ziel ähnlich bevölkerter Wahlkreise erreichen lässt, und zwar ohne Qualitätseinbußen im Ziel der Verwaltungsgrenzen hinnehmen zu müssen. Beide Bewertungskriterien können gleichzeitig sehr gut erfüllt werden.
Dass die derzeit geltenden Wahlkreise keine Optimallösung bilden, ist natürlich nicht Ausdruck gezielter Manipulationen, sondern ergibt sich aus der Komplexität des Problems, das per Hand schlichtweg nicht optimal lösbar ist. Der Bundeswahlleiter setzt daher gerade jetzt auf unsere Ergebnisse. Denn es gilt, ein akutes Problem zu bewältigen: die Größe des Bundestages. Der wächst von Wahl zu Wahl und muss mittlerweile 709 Abgeordnetinnen und Abgeordneten Platz bieten – weit mehr als die im Gesetz genannte Soll-Mitgliederzahl von 598. Im Auftrag des Wahlleiters haben wir daher auf der Basis unserer Forschung Karten mit 270, 250, 200 und 125 möglichst fairen Wahlkreisen erstellt. „Die optimierungsbasierten Wahlkreiseinteilungen sind“, so Bundeswahlleiter Georg Thiel, „ein essenzieller Bestandteil der Bemühungen um eine Wahlrechtsreform.“
Von Politikerinnen und Politikern werden unsere Wahlkreise hingegen teils kritisch begutachtet. Immerhin ändert eine große Reform der Wahlkreisgrenzen deren politische Heimat und womöglich ihre Chancen auf eine Wiederwahl. Im Fall einer Reduktion der Wahlkreisanzahl kann ein Argument unserer Arbeit allerdings schwer übertroffen werden: Die Wahlkreise werden objektiv und nur anhand der Vorgaben aus Recht und Gesetz mathematisch optimal berechnet sein.
Krumme Touren
In den USA legen Regierungen die Wahlkreise fest – und lassen sich dabei ziemlich unverblümt von parteipolitischen Interessen leiten
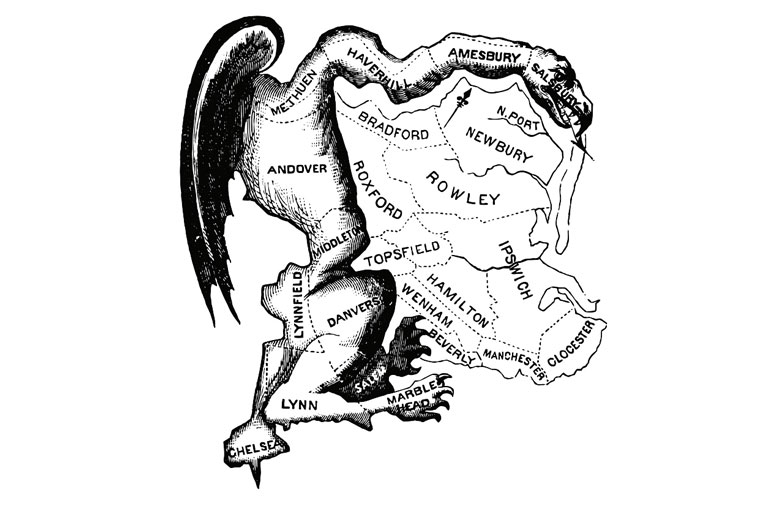
Am Ende schaffte es Elbridge Gerry (1744 – 1814) immerhin noch bis zur Vizepräsidentschaft. Er hatte als einer der Unterzeichner der amerikanischen Unabhängigkeitserklärung zwar großes Ansehen genossen, war dann aber als Gouverneur von Massachusetts eine, wie viele Zeitgenossen urteilten, ziemlich krumme Tour gefahren: Er hatte die Grenzen eines Wahldistrikts bei Boston derart verändert, dass seine Demokratisch-Republikanische Partei davon profitierte. In einer Zeitung erschien daraufhin eine Karikatur, in der die Karte aussah wie ein „Salamander“.
Und so entstand ein Kofferwort, das bis heute vor allem in den USA regelmäßig in aller Munde ist: Gerrymandering (von Gerry und Salamander). Dort werden die Wahlkreise alle zehn Jahre neu festgelegt. Dies geschieht allerdings nicht vonseiten einer politisch neutralen Stelle, sondern durch die Regierung des jeweiligen Bundesstaates. Und die tut dies ganz in ihrem eigenen Sinne.
Dabei scheuen die Verantwortlichen auch vor mitunter üblen, gleichwohl legalen Tricks nicht zurück. So werden große Gefängnisse gerne den Wahlkreisen zugeschlagen, deren Einwohnerzahl ansonsten für einen eigenen Wahlkreis nicht aus- reichen. Da Inhaftierte aber fast nirgends wählen dürfen, entscheidet demnach eine relativ kleine Zahl von wahlberechtigten Bürgerinnen und Bürgern letztlich über eine überproportionale Zahl von Abgeordnetinnen und Abgeordneten. Vor allem die Republikaner profitieren von dieser Praxis in dünn besiedelten ländlichen Regionen.
In Deutschland werden die Wahlkreise hingegen vom Gesetzgeber, dem Bundestag, festgelegt. Zwar ist das Verhältniswahlrecht für das Gerrymandering wenig anfällig, wegen der Grund-, Direkt- und Überhangmandate ist es aber auch hierzulande nicht ganz ausgeschlossen. So fürchteten Vertreter der PDS, als 2001 in Berlin die Bundestagswahlkreise neu zugeschnitten wurden, die ehemaligen Bezirke im West- und Ostteil der Stadt würden derart zusammengelegt, dass die Partei dort kaum Direktmandate erringen könne.
— JS